Page 48 - AV-201712
P. 48
技术
小型房间的声学分区及特性概述
扫一扫 随身阅读
编译/胡楠
在自由场中对点声源的计算或无阻 个例子中分界点频率约为26Hz。而A区和B
碍球面传播的计算相比于房间内部的声学 区的分界点频率计算公式为f=1905√(T/
计算要简单许多。我们一般认为,人耳可 V),其中T代表房间的混响时间,而V代
听的频响范围是20-20kHz,在如此宽的 表房间容积。假设该房间混响时间为0.5
频带中,不同频段在房间中的传播表现形 秒,通过计算我们可以得出A区与B区的分
式是不一样的。对于低频区域来讲,房间 界点约为107Hz。一般来说B区与C区的分
混响对于房间声学特性起主要作用,而在 界线频率约为4f,在这个例子当中我们可
高频段,线性传播方式将对房间声学特性 以得出大约为428Hz。这样我们就将这个
起主要影响。如此宽的频带,不同的频率 小房间分为了4个部分:X区0-26Hz,A
混合,表现形式不一,将会对我们了解房 区26-107Hz,B区107-428Hz,C区408-
间的声学特性造成困扰,计算变得相当复 20000Hz。
杂。由此我们应当将全频域分段,单独进 正如上文所说我们需要对不同区域运
行计算,以便了解房间声学特性。 用不同的计算方式进行计算。除了X区以 图2
当我们面对一个小型房间时,我们可 外,因为该区域的划定完全取决于房间最 来说只有10%左右的语言信息会在200Hz以
以很容易的将房间频响分为四个部分(图1): 长边的长度和声速。对于A区,B区,C区 下的地方,当然,这只是其中一部分的问
第一部分:自由区(X区) 的分界线(f以及4f)我们需要强调,该分 题。
第二部分:典型区(A区) 界点只是通过一个数学模型区进行分区, A区(典型区)随着房间体积的增大
第三部分:混合区(B区) 方便我们之后的计算,而非在这个分界线 而减小,这意味着,越小的房间中,越多
第四部分:线性区(C区) 两端,声音的表现将完全不同。他们之间 的可听到的频率将会遵循点声源扩散的特
的改变是连续过渡的。 性进行传播,也有更多的模态共振产生。
模态共振的次数会随着由A区到C区的 这同时意味着,将有更多的稳态响应区
过渡而增加,但在X区却基本没有。这并不 间,会造成更严重的声染色以及更多频段
意味着在X区(344/2L及以下频率)内的 上的不规则性房间响应。B区(混合特性
频率不存在于房间内,而是向我们指出, 区),也会随着空间的减小而增加。当然
在这个区域的频率并不会对房间频率响应 在B区占主导的衍射及扩散特性相较于A区
造成很大影响。 的模态共振还有很大的不同,这些也会成
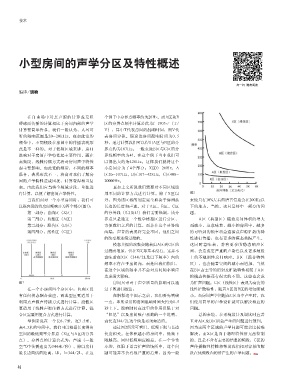
图1 房间尺寸对于声学质量的影响可以通 为扩声问题。C区(线性区)表现为高度的
在一个小房间四个分区中:自由区没 过下图进行概览: 线性扩散特性,随着A区及B区的增加而减
有任何模态耦合效应,而典型区更适用于 在解释这个图示之前,我们要先明确 小,当房间声学问题在C区当中产生时,我
利用点声源声传播方式进行计算,线性区 一点,即所采用的房间混响时间大约为0.5 们使用简单的声学设计就可以解决相应的
更适用于线性声源传播方式进行计算。混 秒上下。混响时间在这里的作用仅限于对 问题。
合区需要用复合方式进行计算。 “阻尼”以及房间吸声系数的一个说明, 总的来说,在系统设计及调试时应着
举例来说在一个长6.7米,宽5.5米, 而长边344/2L这个值是必须知道的。 重对A区及B区所会产生的问题进行预判。
高4.3米的空间中。我们可以根据长度得出 通过图2所示可看出,低频下限与长边 因为这两个区域的声学问题可能会比较难
空间的最低频率分界点(X区与A区的分界 长度相关。在体积越小的房间中,低频下 解决。而X区是由于物理特性所无法控制
点)。分界点的计算公式为:声速(一般 限越高,同时低频响应越差。在一个非常 的,且是不含有主要的信息的频段,C区的
空气中传播速度为344米/秒),除以房间 小的,仅限于语言扩声的场所中,这个问 声传播物理特性将帮助我们相对容易的解
最长边两倍的距离,即:f=344/2L。在这 题可能并不会有很严重的后果,因为一般 决在该频段内的所产生的声学问题。
46