Page 25 - AV_202310

策划

时狂提这个频段的 EQ 也觉得没啥用，完成的作品放到
其它地方一听，糟糕，低频怎么这么多！
后墙抵消现象很可能就是“大坑”的元凶。究竟是
不是，赶紧使用上面说的 1/4 波长结论来计算验证一下
就知道了。如果你成功抓到了元凶，那就赶紧调整音箱
到后墙的距离来改善一下吧！

2、原因详解
声波受到后墙的反射而产生的频率抵消现象，是一
个简单、直接的物理声学现象。那些关于声波、声速、
波长和频率之间的关系、波的反射、波的相位、声波辐
射的指向特性等等校园里曾经学习过的基础知识，是回 什么情况会造成这一对直达声波与反射声波的相位相
答这个问题的基础。 反？当声程差（声音走过的路程的差值）等于 1/2、3/2、
5/2、7/2……[(2n-1)/2] 倍波长的时
候。
声程差是多少？产生在哪里？下图
标示得很清楚，对于你与音箱之间的位
置关系来说，反射声比直达声多走了两
次蓝线的路程，也就是 2 倍的音箱到后
墙的距离（d）。
那么，将 “声程差 = 二分之一的
波长”用公式简单地表述出来，就是：
2d = 1/2 λ（d 代表音箱前脸到后
墙的距离，λ 代表声波波长）
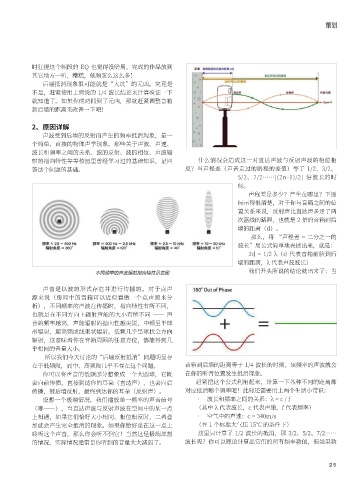
不同频率的声波辐射指向特性示意图 我们开头所说的结论就出来了：当

声音是以波的形式存在并进行传播的。对于点声
源来说（房间中的音箱可以近似看做一个点声源来分
析），不同频率的声波在传播时，指向特性有所不同，
也就是在不同方向上辐射声能的大小有所不同 —— 声
音的频率越高，声能辐射的指向性越尖锐，中频呈半球
形辐射，超高频成线束状辐射。低频几乎呈球状全方向
辐射，这意味着你在音箱周围的任意方位，都能得到几
乎相同的音量大小。
所以我们今天讨论的“后墙反射抵消”问题明显存
在于低频段，而中、高频段几乎不存在这个问题。 音箱到后墙的距离等于 1/4 波长的时候，该频率的声波就会
你可以将声音的低频部分想象成一个大圆球，它既 在你的听音位置发生抵消现象。
会向前传播，直接到达你的耳朵（直达声），也会向后 赶紧把这个公式利用起来，计算一下各种不同的距离都
传播，被后墙反射，最终到达你的耳朵（反射声）。 对应抵消哪个频率吧！此时还需要用上两个生活小常识：
设想一个极端情况，我们播放单一频率的声音信号 • 波长和频率之间的关系：λ = c / f
（嘟——），当直达声波与反射声波在空间中的某一点 （其中 λ 代表波长，c 代表声速，f 代表频率）
上相遇，如果它们恰好大小相同、相位相反时，二者叠 • 空气中的声速：c = 340m/s
加就会产生完全抵消的现象。如果你恰好坐在这一点上 （在 1 个标准大气压 15℃ 的条件下）
聆听这个声音，那么你会听不到它！当然这是极端理想 这里只计算了 1/2 波长的抵消，那 3/2、5/2、7/2……
的情况，实际情况通常是你听到的音量大大减弱了。 波长呢？你可以理论计算出它们的所有频率数值，但如果数

25